Microstructure Evolution
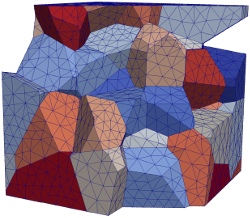
One of recent goals of computational materials science is to predict the evolution of material microstructure in industrially-relevant conditions. Simulations should to be capable of modelling, e.g., dynamic recrystallization and recovery during hot rolling, or the embrittlement of a material in reactor vessel conditions. This would ideally be satisfied by a single code with realistic grain boundary energies and mobilities, point defect generation from radiation damage, diffusion and interaction of solute species, heat evolution and transfer, and anisotropic crystal plasticity. Practically speaking, this is well beyond our current capabilities, and most computational materials science research instead focuses on one of the capabilities above. Cellular Automata Monte Carlo (MC) and cellular automata (CA) simulations comprise a group of computational methods that has been successfully used to study microstructure evolution by grain boundary motion, driven by the reduction of either the grain boundary energy or the stored strain energy. The microstructure is represented at a length scale above that of atoms and below that of grains by a set of discretized volume elements known as voxels. A variety of physical processes can be modeled by manipulating variables attached to the voxels, with the representation otherwise remaining invariant. Our contribution to these models has been to more clearly establish the connection with observed phenomenological rules, enabling more direct comparison of simulations and experiments. Finite Elements One disadvantage of MC and CA simulations is that grain boundary geometries are required to be compatible with the underlying voxel lattice, possibly biasing the evolution of the microstructure. Front-tracking simulations instead represent the grain boundaries by a triangulated surface mesh and allow arbitrarily complicated configurations, but can be significantly more difficult to implement because the topological transitions must be handled explicitly. We are currently using our previous experience with front-tracking simulations to develop a finite element simulation (shown on the right) that (1) uses a volumetric mesh to allow the eventual inclusion of arbitrary material physics, (2) significantly expands the set of allowed topological transitions to allow for general grain boundary network dynamics, and (3) proposes an energy dissipation criterion to select a topological transition in a system with an arbitrary grain boundary energy. |
Structural Descriptors
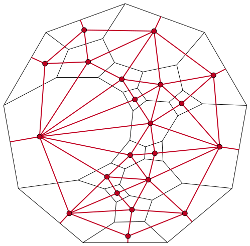
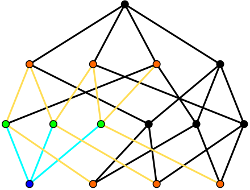
The vision of rational materials design involves starting with the desired material properties, and then using computational techniques to design compatible microstructures and identify practical processing routes to fabricate the materials. This presumes the availability of microstructure descriptors that are that are detailed enough to tightly constrain the material properties, and yet are generic enough to not distinguish between samples fabricated by the same processing procedure. Part of our research involved developing such structural descriptors to accelerate progress toward the rational design of materials. Topological Roundness While the geometry of the grains contributes to many of the properties of polycrystalline materials, a grain’s geometry can be difficult to describe succinctly. One alternative is to give an average length scale along with the topology of the grain, i.e., the connectivity of the grain boundaries, junction lines, and junction points on the grain’s surface. This does not allow an exact reconstruction of the grain, but is a manageable amount of information and still describes the way the grain is connected to its surroundings. We have developed a convenient encoding of this topology by means of Weinberg vectors, and recently proposed a notion of combinatorial roundness as the topological counterpart to geometric roundness. Swatches and Cloths A cell complex is a general object that can be used to describe a variety of physical systems. It is constructed by placing any necessary 0-cells (points), attaching the endpoints of deformed 1-cells (line segments) to the 0-cells, attaching the boundaries of deformed 2-cells (disks) to the 1-cells, and attaching the surfaces of deformed 3-cells (balls) to the 2-cells. This allows the description of, e.g., atomic systems with atoms as 0-cells and bonds as 1-cells, or polycrystals with junction points as 0-cells, junction lines as 1-cells, boundaries as 2-cells, and grains as 3-cells. A swatch completely characterizes the local topology of a small region of the cell complex, as for the cell complex of a solid tetrahedron on the right. The set of frequencies of the various swatch types occurring in the cell complex is known as the cloth. This description is complete in the sense that any question about the local topology can be answered from the cloth, and general in that any physical system that can be represented as a cell complex is admissible. Our current research involves including some geometric information in the cloth and extending the set of situations where the cloth can be calculated. |
Atomic Systems
|
Molecular Dynamics
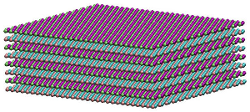
Molecular Dynamics (MD) is a standard technique to simulate the behavior of atomic systems, and is particularly useful when the relevant physical mechanisms are not known. The behavior of any MD simulation is governed by a function known as the interatomic potential that describes the contribution of neighboring atoms to the overall potential energy, and is generally assumed to have an analytic form. Our group has developed several interatomic potentials (including for the hexagonal boron-nitride nanoparticle to the right) to study the thermal properties of nanofluids which are attractive for next-generation heat transfer applications. Requiring the interatomic potential to be analytic has the disadvantages of limited accuracy (only some material properties can be reproduced) and inflexibility (a potential developed for diamond is usually not appropriate for graphite) though. This means that MD can have difficulty reproducing, e.g., phase transitions, even when the interatomic potential is specifically designed for this purpose. We are working to overcome this limitation by developing flexible neural network potentials to computationally assess phase stability and identify fabrication procedures in experimentally relevant conditions. BBGKY hierarchy Molecular dynamics is generally restricted to time steps shorter than the atomic vibration period, limiting the overall simulation length. As an alternative, a statistical mechanical approach can be used to follow the time-averaged motion of atoms and simulate longer periods. This is the motivation for the dynamic density function theory (DDFT) of fluids and the phase field crystal model (PFCM), though DDFT is restricted to very specific particle systems, and several studies have questioned the accuracy of the PFCM. Our approach is instead to start with a dynamic form of the BBGKY hierarchy for multiple-particle distribution functions and develop a closure relation. The result is a method that has rigorous theoretical underpinnings and can simulate systems with arbitrary interatomic potentials. The simulation to the right shows the localization of atoms as the solid forms from a supercooled liquid. |
Orientation Information
The texture of a polycrystalline material is the probability distribution of the crystallite orientations, generally weighted by volume fraction. Texture is used to predict macroscopic material properties by averaging the properties of anisotropic single crystals, affects the performance of a catalyst by indicating the crystallographic planes exposed on the material surface, and provides a standard means to measure the extent of deformation processes. Mathematically, a texture is a probability distribution function on the space of three-dimensional rotations, and therefore requires some choice for the parameterization of the space. The traditional choice is a set of three Euler angles, since this parameterization is particularly convenient when using a goniometer for X-ray diffraction measurements. Nevertheless, manipulating texture information in this parameterization is difficult. We propose that a texture may be more advantageously considered as a probability distribution on the space of normalized quaternions. This is justified not only by the particularly favorable mathematical properties of quaternions, but by the ability to visualize a texture in the same axis-angle parameterization that is used in crystallography. Recently, we have begun to extend these ideas to grain boundaries as well, though the space of grain boundaries is more complicated and less well-studied than that of crystallographic orientations. |